BÀI . PHÉP ĐỒNG DẠNG
I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa:
Phép biến hình F được gọi là đồng dạng tỉ số k (k >0) nếu với 2 điểm bất kỳ M, N và ảnh M’, N’ ta có: M’N’ = kMN
Phép dời hình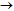 
phép đồng dạng k = 1
Phép vị tự 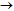phép đồng dạng |k|
2. Tính chất:
Phép đồng dạng
Biến 3 điểm thẳng hàng 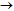3 điểm thẳng hàng
Biến đường thẳng 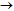đường thẳng
Biến tia 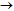tia
Biến đường thẳng 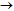đường thẳng mà độ dài nhân lên k lần
Biến D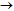D đồng dạng với nó
Biến đường tròn 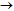đường tròn có bán kính R’ = kR
Biến góc thành góc bằng chính nó.
3. Hình đồng dạng:
Hai hình được gọi là đồng dạng nếu có phép đồng dạng biến hình này thành hình kia.
Mỗi phép đồng dạng tỉ số k (k >0) đều là hợp của 1 phép vị tự tỉ số k và một phép dời hình.
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Bài 1 – SGK: Cho D ABC, xác định ảnh qua phép đồng dạng có được bằng cách thực hiện liên tiếp V(B;1/2) và đường trung trực BC.
Bài 2. Cho điểm M, điểm O, đường thẳng a dựng ảnh của phép đồng dạng F là hợp thành của phép vị tự đối xứng trục Đa và phép vị tự V(O,2) O 
a trong các trường hợp:
a . M
a
b .M a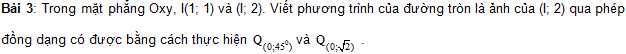
Bài 4. Trong mặt phẳng Oxy cho d: x + y + 2 = 0. Viết phương trình d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp V(I) phép vị tự tâm I(0; 1) và tỉ số k = 2 và phép quay tâm O, góc -450.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho DABC có đường cao AH. H ở trên đoạn BC. Biết AH = 4, HB = 2, HC = 8. Phép đồng dạng F biến DHBA thành DHAC. F được hợp thành bởi hai phép biến hình nào dưới đây?
A . Phép đối xứng tâm H và phép vị tự tâm H tỉ số k = 1/2.
C .Phép vị tự tâm H tỉ số k = 2 và phép quay tâm H, góc (HB; HA)
D .Phép vị tự tâm H tỉ số k = 2 và phép đối xứng trục.
Hướng dẫn giải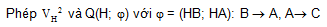
Vậy: F là phép đồng dạng hợp thành bởi V và Q biến DHBA thành DHAC.
Bài 2. Cho hình bình hành ABCD có tâm O. Trên cạnh AB lấy điểm I sao cho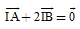 
và gọi G là trọng tâm của DABD. F là phép đồng dạng biến DAGI thành DCOD. F được hợp thành bởi hai phép biến hình nào sau đây?
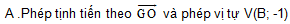
B .Phép đối xứng tâm G và phép vị tự V(B; 1/2).
C .Phép vị tự V(A; 3/2 ) và phép đối xứng tâm O
D .Phép vị tự V(A; 2/3 ) và phép đối xứng tâm G
Hướng dẫn giải.
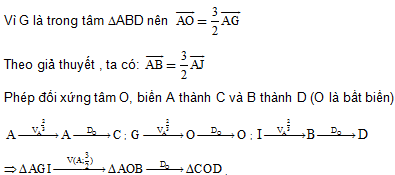
Bài 3. Cho hai đường thẳng a và b cắt nhau và điểm C. Tìm trên a và b các điểm A và B tương ứng sao cho tam giác ABC vuông cân ở A.
Hướng dẫn giải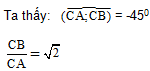
Do đó có thể xem B là ảnh của A qua phép đồng dạng F có được bằng cách thực hiện liên tiếp phép quay tâm C góc -450 và phép vị tự tâm C, tỉ số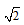 
Vì AÎa, nên BÎa’’ = F(a), B Îb
Nên B là giao của a’’ với b
Bài 4. Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y -2 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I(-1; -1) tỉ số k = 1/2 và phép quay tâm O góc – 450.
Hướng dẫn giải.
Gọi d1 là ảnh của d qua phép vị tự tâm I(-1; -1) tỉ số k = 1/2 . Vì d1 song song hoặc trùng với d nên phương trình của nó có dạng: x + y + C = 0
Lấy M(1; 1) thuộc d, thì ảnh của nó qua phép vị tự nói trên là O thuộc d1.
Vậy phương trình của d1 là: x + y = 0. Ảnh của d1 qua phép quay tâm O góc -450 là đường thẳng Oy. Vậy phương trình của d’ là x= 0.