BÀI. PHÉP BIẾN HÌNH (TIẾT 1)
I. TÓM TẮT LÝ THUYẾT
1. Phép biến hình:
Định nghĩa: Phép biến hình là 1 quy tắc để với mỗi điểm M của mặt phẳng xác định duy nhất M’ của mặt phẳng đó.
Kí hiệu: phép biến hình f.
M’ = f(M)
M: tạo ảnh (gốc)
M’: ảnh.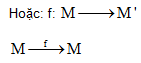
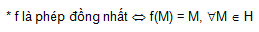
 tạo thành 1 hình H’ được gọi là ảnh của H
tạo thành 1 hình H’ được gọi là ảnh của H
qua phép biến hình f
Ký hiệu: H’ = f(H)
Chú ý: Mỗi điểm M chỉ có duy nhất 1 ảnh M’.
Có thể có nhiều điểm khác nhau cho chung 1 ảnh.
Phép biến hình:
+ Không thay đổi khoảng cách.
+ Có thể thay đổi khoảng cách.
2. Phép dời hình:
Định nghĩa: phép dời hình là 1 phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ.
Tức là, với 2 điểm M, N và ảnh của chúng M’, N’ ta luôn có: M’N’ = MN
Tính chất của phép dời hình
Ba điểm thẳng hàng thành 3 điểm thẳng hàng cùng thứ tự
Đường thẳng 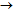 đường thẳng.
đường thẳng.
Đoạn thẳng 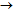 đoạn thẳng bằng chính nó.
đoạn thẳng bằng chính nó.
Tia thành tia
Tam giác 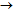 tam giác bằng chính nó.
tam giác bằng chính nó.
Góc thành góc bằng chính nó
Đường tròn 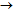 đường tròn cùng bán kính.
đường tròn cùng bán kính.
3. Phép biến hình hợp:
Thực hiện 2 phép biến hình liên tiếp ta được một phép biến hình gọi là hợp thành của 2 phép biến hình.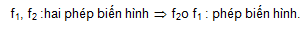
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
VĐ 1: Một quy tắc đặt trong mặt phẳng là 1 phép biến hình
Phương pháp: Dựa vào định nghĩa (không phân loại)
Bài 1: Trong mặt phẳng Oxy cho phép biến hình biến một điểm M(x; y) thành M’(x’; y’) sao cho 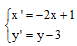 . Tìm
. Tìm
ảnh của các điểm sau:
a. A(1; 2) b. B(-1; 2) c. C(2; 0)
Bài 2. Trong mặt phẳng Oxy cho phép biến hình: f: M(x; y) 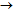 M’ = f’(M) = (x + 1; y – 2)
M’ = f’(M) = (x + 1; y – 2)
a . Tìm ảnh của A(0; 2) ; B(3; -1)
b. Chứng minh rằng: f là 1 phép dời hình.
Bài 3. Chứng minh rằng phép biến hình của (B2) không phải là phép dời hình.
Bài 4. Cho điểm O. Với mỗi điểm M ta dựng điểm M’ sao cho OM’ = 2OM. Quy tắc đặt mỗi điểm M với M’ như trên
có phải là phép biến hình không?
Bài 5. Trong mặt phẳng Oxy cho phép biến hình f thỏa f: M(x; y) 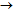 M’ = f(M) = (3x; y + 1). Tìm ảnh của
M’ = f(M) = (3x; y + 1). Tìm ảnh của
a. A(0; 1) b. B(2; 2) c. C(-2; 1).
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Trong mặt phẳng Oxy cho phép biến hình f: 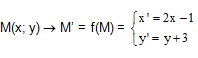 .
.
Tìm ảnh của các điểm sau: a. A(1; 2) b. B(-1; 2) c. C(2; -4).
Bài 2. Trong mặt phẳng Oxy cho phép biến hình f: M(x; y) 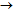 M’ = f(M) = (-2x; y + 1). Tìm ảnh của đường thẳng (D): x – 3y – 2 = 0 qua phép biến hình f.
M’ = f(M) = (-2x; y + 1). Tìm ảnh của đường thẳng (D): x – 3y – 2 = 0 qua phép biến hình f.
Bài 3. Trong mặt phẳng Oxy cho phép biến hình f: M(x; y) 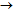 M’ = f(M) = (x + 3; y + 1)
M’ = f(M) = (x + 3; y + 1)
a. Chứng minh rằng f là phép biến hình.
b. Tìm ảnh của đường tròn (C): (x + 1)2 + ( y -2)2 = 4.
Bài 4. Trong mặt phẳng Oxy cho phép biến hình f: M(x; y) 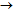 M’ = f(M) = (x/2 ; -3y). Khẳng định nào sau đây sai?
M’ = f(M) = (x/2 ; -3y). Khẳng định nào sau đây sai?