CHỨNG MINH BA ĐIỂM THẲNG HÀNG
I.TÓM TẮT LÝ THUYẾT
Để chứng minh ba điểm A, B, C thẳng hàng ta chứng minh ba điểm đó thoả mãn đẳng thức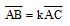 
với k ≠ 0.
Để chứng minh hai điểm M, N trùng nhau ta chứng minh chúng thoả mãn đẳng thức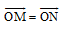 
, với O là một điểm nào đó hoặc 
.
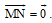II. PP GIẢI BÀI TẬP
Bài 1. Cho bốn điểm O, A, B, C sao cho :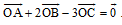
. Chứng tỏ rằng A, B, C thẳng hàng.
Bài 2. Cho tam giác ABC, gọi G, H, O lần lượt là trọng tâm, trực tâm và tâm đường tròn ngoại tiếp tam giác ABC. CMR 3 điểm G, H, O thẳng hàng.
Bài 3. Cho hình bình hành ABCD. TrênBC lấy điểm H, trên BD lấy điểm K sao cho: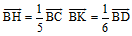
. Chứng minh: A, K, H thẳng hàng.
Bài 4. Cho DABC với I, J, K lần lượt được xác định bởi: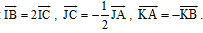 
Bài 5. Cho hình bình hành ABCD. Trên các tia AD, AB lần lượt lấy các điểm F, E sao cho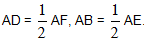 
. Chứng minh:
a. Ba điểm F, C, E thẳng hàng.
b. Các tứ giác BDCF, DBEC là hình bình hành.
Bài 6. Cho DABC. Hai điểm I, J được xác định bởi: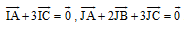 
. Chứng minh 3 điểm I, J, B thẳng hàng.
Bài 7. Cho tam giác ABC. Các điểm M, N được xác định bởi các hệ thức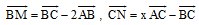 
. Xác định x để A, M, N thẳng hàng.
Bài 8. Cho DABC. Gọi A‘, B‘, C‘ là các điểm định bởi: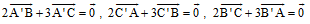 
Chứng minh các tam giác ABC và A‘B‘C‘ có cùng trọng tâm.
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho tam giác ABC. Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho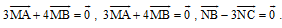 
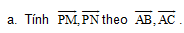
b. Chứng minh ba điểm M, N, P thẳng hàng.
Bài 2. Cho DABC. Hai điểm M, N được xác định bởi: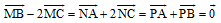 
Chứng minh 3 điểm M, G, N thẳng hàng, với G là trọng tâm của DABC.
Bài 3. Cho DABC. Lấy các điểm M N, P: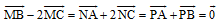 
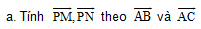
b. Chứng minh 3 điểm M, N, P thẳng hàng.