BÀI 4. BẤT ĐẲNG THỨC BU-NHIA-CỐP-XKI
I. TÓM TẮT LÝ THUYẾT
II. BÀI TẬP ÁP DỤNG
Bài 1. Chứng minh các bất đẳng thức sau:
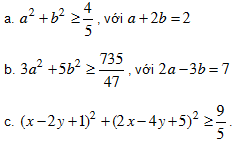
Bài 2. Chứng minh rằng: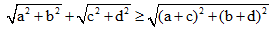 
Bài 3.
a. Chứng minh rằng: |ab + bc + ca| ≤ a2 + b2 + c2
b. Cho a, b, c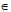 
R {0}. Chứng minh: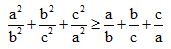 
c. Cho a, b 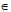R, thỏa mãn a3 + b3 = 2. Chứng minh : a2 + b2 ≤ 2
Bài 4. Chứng minh các bất đẳng thức sau:
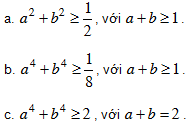
Bài 5. Cho
III. BÀI TẬP ĐỀ NGHỊ
Bài 1. Chứng minh các bất đẳng thức sau:
a. 3a2 + 4b2 ≥ 7, với 3a + 4b = 7
b. 2a2 + 3b2 ≥ 5 , với 2a + 3b = 5
Bài 2. Chứng minh các bất đẳng thức sau:
