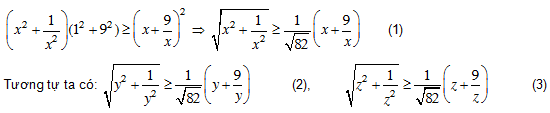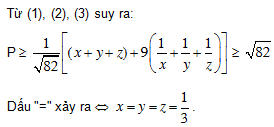BÀI 7. BÀI TẬP NÂNG CAO VỀ BẤT ĐẲNG THỨC
I .TÓM TẮT LÝ THUYẾT
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Bài 1. Cho a, b, c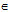 
R. Chứng minh các bất đẳng thức sau:
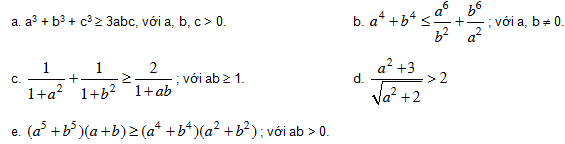
Bài 2. Cho a, b ≥ 0 . Chứng minh bất đẳng thức: a3 + b3³ a2b + b2a = ab(a + b) (1). Áp dụng chứng minh các bất đẳng thức sau:
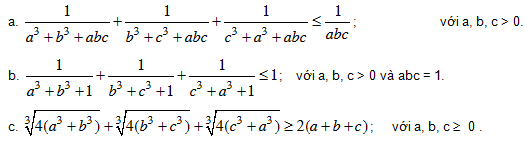
Bài 3. Cho ba số không âm a, b, c và a + b +c ≤ 3. Chứng minh :
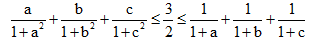
Bài 4. Cho x, y > 0. Chứng minh rằng: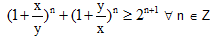 
Bài 5. Tìm giá trị lớn nhất của hàm số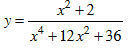 
III. BÀI TẬP ĐỀ NGHỊ
Bài 1.
a. Cho a, b > 0. Chứng minh: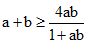 
Hd : sử dụng BĐT Côsi cho hai số dương a, b và 1 + ab
b. Cho x ≥ 1, y ≥ 1. Chứng minh: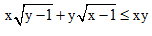 
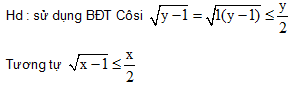
c. Cho a, b, c Î R, thỏa mãn a + b + c = 1. Chứng minh: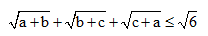 
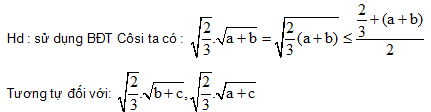
Bài 2. Cho a, b, c > 0. Chứng minh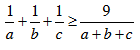 
(1). Áp dụng chứng minh các BĐT sau:
a. Cho a, b, c > 0 thoả a + b + c ≤ 1. Tìm GTNN của biểu thức:
.
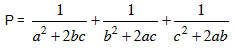b. Cho a, b, c > 0 thoả a + b + c = 1. Chứng minh: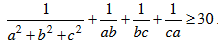 
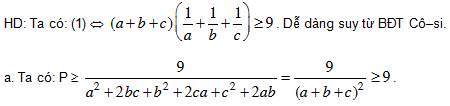
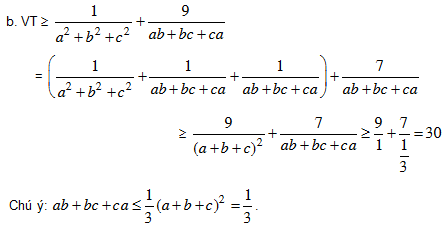
Bài 3. Cho x, y, z là ba số dương và x + y + z ≤ 1. Chứng minh rằng:
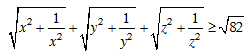
HD: Áp dụng BĐT (B), ta có:
